Jednym z błędów często popełnianych przez początkujących programistów Javy jest używanie niepoprawnych typów do reprezentowania i operowania na kwotach.
Jako że kwota jest liczbą z dwoma miejscami po przecinku, to intuicyjne podeście sugeruje użycie typu liczby zmiennoprzecinkowej, jak double albo float. Niestety jest to podeście złe, ponieważ typy zmiennoprzecinkowe ze swojej natury są nieprecyzyjne, tzn. zapisując wartość 0.01 nie mamy gwarancji że kompilator nie użyje w reprezentacji wewnętrznej wartości 0.010000001. Pamiętam ze studiów, że któryś z wykładowców posłużył się tu ładnym przykładem, że typy zmiennoprzecinkowe doskonale nadają się do reprezentowania danych fizycznych, jak ciężar, odległość, temperatura, itp. Ta drobna różnica na końcu jest pomijalna ponieważ zawsze jest znacznie mniejsza od dokładności pomiaru.
Jednak kwoty to nie pomiar fizyczny, tylko bardzo konkretne wartości o ściśle ustalonej precyzji. Nieprawidłowe zaokrąglenie lub „wielokrotne” dodanie takiej zaokrąglonej kwoty to bardzo poważny błąd biznesowy i straszny sen bankowców.
Niepoprawne użycie typu double
Spójrzmy na przykład produktu którego cena wynosi 9,99 netto, do którego chcemy dodać podatek VAT w wysokości 23% i obliczyć wartość zamówienia na 10.000 sztuk. Następnie dla testu obliczymy wartość netto całości zamówienia. Niepoprawna implementacja w oparciu o typ double wygląda tak:
double priceWithoutVat = 9.99;
log.info("Price without VAT: {}", priceWithoutVat);
double priceWithVat = priceWithoutVat * 1.23;
log.info("Price with VAT: {}", priceWithVat);
double valueWithVat = priceWithVat * 10000;
log.info("Value with VAT: {}", valueWithVat);
double priceWithoutVat2 = valueWithVat / 1.23;
log.info("Value without VAT: {}", priceWithoutVat2);
Wynik działania takiego programu wygląda tak:
Price without VAT: 9.99 Price with VAT: 12.287700000000001 Value with VAT: 122877.00000000001 Value without VAT: 99900.00000000001
Program zasadniczo działa, jednak każdy intuicyjnie czuje że zaprezentowanie takich kwot na ekranie koszyka będzie wyglądać źle. Więc niedoświadczony programista może brnąć dalej: trzeba tak sformatować wartość tak aby „ukryć” niepotrzebną końcówkę:
String priceWithVatRounded = String.format("%.2f", priceWithVat);
log.info("Price with VAT: {}", priceWithVatRounded);
W efekcie otrzymamy taki wynik:
Price with VAT: 12,29
Wygląda nawet fajnie, ale jak widać wartość została zaokrąglona w górę. Problem polega na tym że nie była to świadoma decyzja programisty tylko „tak wyszło”. A przypadku poważnych systemów finansowych każda taka decyzja powinna być podejmowana zgodnie z regułami księgowości…
Ciekawy pomysł z użyciem typu int
Przeglądając kod innego programisty (pozdrawiam Martę ;-)) znalazłem ciekawy pomysł z użyciem do reprezentacji kwot typu stałoprzecinkowego int. Pomysł polegał na tym, żeby pamiętać, że kwota jest zawsze pomnożona przez 100 tak aby część groszowa była zawarta w części całkowitej. I przed samym wyświetleniem użytkownikowi podzielić ją z powrotem przez 100 żeby przesunąć część groszową z powrotem na prawo od przecinka. Kod dla wcześniej opisanego przykładu wyglądałby tak:
int priceWithoutVat = 999;
log.info("Price without VAT: {}", priceWithoutVat/100f);
int priceWithVat = priceWithoutVat * 123;
log.info("Price with VAT: {}", priceWithVat/100f/100f);
int valueWithVat = priceWithVat * 10000;
log.info("Value with VAT: {}", valueWithVat/100f/100f);
int priceWithoutVat2 = valueWithVat / 123;
log.info("Value without VAT: {}", priceWithoutVat2/100f);
Wynik działania programu z kolei wygląda tak:
Price without VAT: 9.99 Price with VAT: 12.287701 Value with VAT: 122877.0 Value without VAT: 99900.0
Jak widać jest lepiej, bo nie ma już problemu dodatkowych wartości daleko po przecinku.
Co ciekawe, tamto użycie było prawidłowe ponieważ dotyczyło tylko operacji mnożenia przez liczby całkowite (ilości pozycji w koszyku). Jak widać na powyższym przykładzie, po pomnożeniu tak przesuniętej kwoty przez drugą wartość procentową, którą też musieliśmy przesunąć, to przed wyświetleniem trzeba pamiętać żeby przesunąć nie o 2 miejsca w prawo tylko już o 4 (podzielić przez 10.000). Jak nietrudno zauważyć, powyższy kod jest mało czytelny i bardzo nieintuicyjny dla kogoś kto nie wie o „pomyśle”.
Użycie typu BigDecimal
Jedynym poprawnym typem do wykonywania operacji na kwotach w „gołej” Javie jest typ BigDecimal (są też dodatkowe biblioteki). Jest to typ pomyślany do reprezentacji liczb o ściśle określonej precyzji i zawierający metody do wykonywania operacji arytmetycznych o ściśle określonym sposobie zaokrąglania wyniku. Analogiczny kod dla powyższego przykładu będzie wyglądać tak:
BigDecimal priceWithoutVat = new BigDecimal("9.99");
log.info("Price without VAT: {}", priceWithoutVat);
BigDecimal priceWithVat = priceWithoutVat.multiply(
new BigDecimal("1.23"));
log.info("Price with VAT: {}", priceWithVat);
priceWithVat = priceWithVat.setScale(2,
BigDecimal.ROUND_HALF_EVEN);
log.info("Price with VAT (2): {}", priceWithVat);
BigDecimal valueWithVat = priceWithVat.multiply(
new BigDecimal(10000));
log.info("Value with VAT: {}", valueWithVat);
BigDecimal priceWithoutVat2 = valueWithVat.divide(
new BigDecimal("1.23"),
BigDecimal.ROUND_HALF_EVEN);
log.info("Value without VAT: {}", priceWithoutVat2);
Wynik działania programu:
Price without VAT: 9.99 Price with VAT: 12.2877 Price with VAT (2): 12.29 Value with VAT: 122900.00 Value without VAT: 99918.70
Jego API na pierwszy rzut wygląda mało czytelnie, ponieważ zamiast oczywistych operatorów typu +, -, * i / są dedykowane metody do każdej operacji i prawdopodobnie dlatego niedoświadczeni programiści unikają jego użycia. Jednak jeżeli się dokładniej mu przyjrzeć to można zauważyć że poszczególne operacje są logiczne i wykonywane świadomie:
- pomnożenie kwoty (precyzja „2”) przez podatek (precyzja „2”) daje kwotę z podatkiem o precyzji „4”,
- powrót do precyzji kwoty (2) wymaga zaokrąglenia metodą
setScaledo której trzeba świadomie podać sposób w jaki zostanie ono wykonane, - operacja dzielenia (
divide), która z natury jest „stratna”, również wymaga świadomego podania sposobu zaokrąglania wyniku.
Operacje zaokrąglania
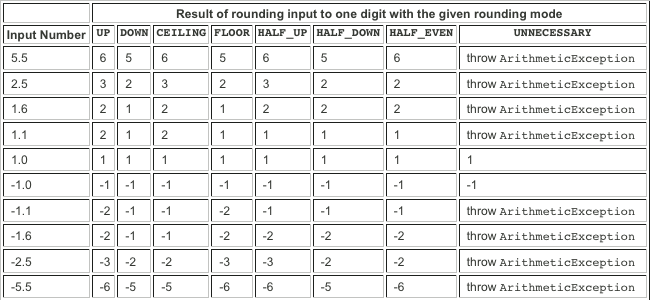
To w jaki sposób wykonywać zaokrąglanie końcówek jest sprawą nietrywialną. Problem można podzielić na dwie części: techniczną i biznesową – zaczniemy od tej pierwszej. Zaokrąglać operacje można w dół lub w górę najlepiej przedstawia dostępne możliwości przykład z javadoca klasy RoundingMode:
W największym uproszczeniu można je opisać tak:
UPiCEILINGzaokrąglają w górę, tylko UP do wartości większej absolutnie, czyli dla wartości ujemnych odwrotnie,DOWNiFLOORprzeciwnie, tzn. zaokrąglają w dół, tylko DOWN do wartości mniejszej absolutnie,HALF_UPiHALF_DOWNodpowiednio od połowy włącznie w górę i od połowy włącznie w dół,HALF_EVENod połowy do najbliższej parzystej.
Szczególnie interesujący jest ostatni, tj. HALF_EVEN określany jako „ulubiony” do operacji finansowych, ponieważ „minimalizuje skumulowany błąd, gdy stosowany jest wielokrotnie do sekwencji obliczeń”.
Jeżeli już wiemy jakie mamy techniczne możliwości wyboru typu zaokrąglania, to należy zadać sobie pytanie „biznesowe” który z nich wybrać. Moja opinia jest taka, że najlepiej znaleźć kogoś mądrzejszego, kto się na tym zna i poprosić jego o decyzje. W przypadku prostych sklepów internetowych może to być biuro księgowe, które będzie obsługiwało nasze faktury. W przypadku systemów bankowych koniecznie decyzję powinni podjąć specjaliści po stronie klienta.
Żeby pokazać jak bardzo może to być skomplikowane, posłużę się przykładem naliczania rabatów do pozycji zamówienia. Wyobraźmy sobie że mamy sklep z narzędziami, a klient zamówił 3 klucze w cenie katalogowej 99,99 zł i 1000 śrubek w cenie 0,07 zł. Wartość całego zamówienia bez rabatu wyniesie dokładnie 369.97 zł. Jest to stały klient który ma 5,6% upustu.
W momencie implementacji decydujące jest w którym miejscu wykonamy naliczanie rabatu. Często jest to związane ze specyfikacją naszej aplikacji wymyśloną przez projektanta lub wymuszoną przez zamawiającego – np. konieczność prezentacji ceny jednostkowej z rabatem. Tutaj kryje się pułapka, ponieważ cena jednostkowa klucza z rabatem wynosi 94.39056, a po zaokrągleniu 94.39, co wygląda jeszcze stosunkowo dobrze. Niestety po naliczeniu rabatu do ceny śrubki jej cena wynosi 0.06608, co po zaokrągleniu daje 0.07 – tutaj różnica jest dosyć znaczna. Do czego to prowadzi? Jeżeli obliczymy wartość łączną zamówienia przez pomnożenie tych cen jednostkowych z rabatem przez ilość i zsumujemy to otrzymamy 353.17. I jak teraz „sprytny” klient weźmie kalkulator do ręki i obliczy jaki faktycznie aplikacja wyliczyła mu rabat, to wyjdzie mu szybko że tylko 5%, a nie 5,6% jak obiecywaliśmy. Czy aplikacja oszukała? Nie, to skutek właśnie tych zaokrągleń.
Alternatywnym sposobem jest obliczanie rabatu od wartości dla danego produktu lub łącznej wartości zamówienia, jednak wtedy cena jednostkowa pomnożona przez ilość pozycji nie będzie równa wartości dla danego produktu… Najlepiej byłoby arbitralnie ustalić że rabat jest naliczany tylko do całkowitej wartości zamówienia ale jak klient się uprze…
Tworzenie obiektów BigDecimal
Przy tworzeniu obiektów klasy BigDecimal jest jeszcze jedna drobna pułapka w którą często wpadają niedoświadczeni programiści, więc warto o niej wspomnieć. Często zdarza się, że musimy stworzyć obiekt reprezentując konkretną wartość, np. jeden grosz (0.01) albo stawkę VAT (np. 1.23). Klasa BigDecimal ma wiele konstruktorów pozwalających na przekazanie wartości jako typy proste. Intuicyjne wydaje się więc przekazanie np. wartości 1.23 jako float. Sporo osób tak robi myśląc, że ustawią w ten sposób oczekiwany poziom precyzji na „2” (dwie cyfry po przecinku).
Spójrzcie więc na poniższy fragment kodu który inicjuje taką samą wartość 1.23 z typu float, double i String:
BigDecimal fromDouble = new BigDecimal(1.23d);
log.info("From double, scale: {}, value: {}", fromDouble.scale(),
fromDouble);
BigDecimal fromFloat = new BigDecimal(1.23f);
log.info("From float, scale: {}, value: {}", fromFloat.scale(),
fromFloat);
BigDecimal fromString = new BigDecimal("1.23");
log.info("From float, scale: {}, value: {}", fromString.scale(),
fromString);
Wynik działania tego programu to:
From double, scale: 51, value: 1.229999999999999982236431605997495353221893310546875 From float, scale: 21, value: 1.230000019073486328125 From float, scale: 2, value: 1.23
Jak widać, konstruktor z użyciem typów zmiennoprzecinkowych ustawił nam precyzję nie na „2”, tylko na wartość specyficzną dla tych typów. Wniosek z tego taki, że mało intuicyjny konstruktor przekazujący napis (String) jest rekomendowany do inicjowania obiektów klasy BigDecimal, bo tylko on jednoznacznie przekazuje poziom precyzji.
I jeszcze jeden tip na koniec: klasa BigDecimal zawiera, podobnie jak Integer, stałe reprezentujące „popularne” wartości z których należy korzystać zamiast tworzyć nowe obiekty przez new: ZERO, ONE i TEN – ich użycie spowoduje źe przy dużej ilości operacji kod będzie szybszy i zajmować mniej pamięci oraz będzie bardziej „elegancki” – Sonar się nie przyczepi :-).
Reasumując: operacje na kwotach to delikatna sprawa i trzeba to robić ostrożnie. I koniecznie używać klasy BigDecimal.


Bardzo przystępne wyjaśnienie, dzięki!